What is PTGL?
Table of contents
Overview
PTGL stands for Protein Topology Graph Library. It is a database of protein structure topologies modeled as undirected, labeled graphs. It provides a web server to visualize and analyze protein structure topologies at different scales, e.g., secondary structure level and chain level. The graph computation was done by our software PTGLtools (formerly labeled VPLG). PTGLtools is based on the 3D atomic coordinates from the PDB either as legacy PDB file or as macromolecular Crystallographic Information File (mmCIF). Reading mmCIFs allows processing large protein structures (> 62 chains or > 99,999 atoms). The secondary structure assignment is parsed with small adaptions from a DSSP file.

Contact definition
We define contacts on different levels of abstraction or scales, respectively.
Atom
Atoms are modelled as hard spheres with a radius of 2 Å for atoms of amino acids and of 3 Å for ligand atoms. An atom-atom contact is defined if two hard spheres overlap. For atoms of amino acids the contact is differentiated depending on the position of the involved atoms in the amino acid backbone or side chain. This yields atom level contacts of the following types:- BB: backbone - backbone contact
- BC: backbone - side chain contact
- CC: side chain - side chain contact
- LB: ligand - backbone contact
- LC: ligand - side chain contact
- LL: ligand - ligand contact
- LX: ligand - non-ligand contact, i.e., LX = LB or LC
Residue
A residue-residue contact is defined if two residues share an atom contact.Secondary structure element
Depending on the type of the secondary structure elements (SSEs), we applied a rule set:| SSE 1 type | SSE 2 type | Required contacts |
|---|---|---|
| Beta strand | Beta strand | BB > 1 or BC > 2 |
| Helix | Beta strand | BB > 1 or BC > 3 or CC > 3 |
| Helix | Helix | BC > 3 or CC > 3 |
| Ligand | Any type | LX >= 1 |
Chain
A chain-chain contact is defined if two chains share atleat one residue-residue contact-Protein Graphs
A Protein Graph is defined as labeled, undirected graph. The vertices correspond to the secondary structure elements or ligands, and they are labeled with the secondary structure element type (alpha helix, beta strand or ligand). The vertices of the Protein Graph are enumerated as they occur in the sequence from the N- to the C-terminus.
The edges of the Protein Graph represent spatial adjacencies of secondary structure elements (see contact definition). According to the direction of the spatical adjacent SEEs, their orientation to each other can be parallel (p), anti-parallel (a), or mixed (m).
Visualization
In the graph visualizations available on the PTGL server, the secondary structure elements are ordered as red circles (helices), black quadrats (strands), or magenta rings (ligands) on a straight line according to their sequential order from the N- to the C-terminus. The spatial neighborhoods are drawn as arcs between secondary structure elements. The edges are colored according to their labeling as parallel (red), anti-parallel (blue), mixed (green) or ligand (magenta). This is the key for the images:
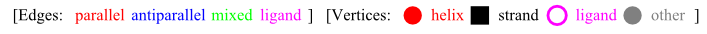
Below the vertices there are the numbers of the secondary structure elements for this type of Protein Graph (PG) and for the occurrence in the sequence of the whole list of secondary structure elements (SQ).
Graph types
If only a certain secondary structure element type is of interest, the graph modelling allows to exclude the non-interesting secondary structure element types. According to the secondary structure element type of interest, the Protein Graph can be defined as an Alpha graph, Beta graph, or Alpha-Beta graph. If you are interested in the ligands as well, you can also use the Alpha-Ligand graph, the Beta-Ligand graph, and the Alpha-Beta-Ligand graph.
The Alpha graph contains only alpha helices and the contacts between them. The Alpha-Beta graph contains alpha helices, beta strands and the contacts betweem them, and so on.
As an example for Protein Graphs and their graph types, we present the structure with PDB ID 7tim [Davenport et al., 1991, Biochemistry].
Alpha Graph
The Alpha-Graph of the protein 7tim chain A consisting of 13 helices.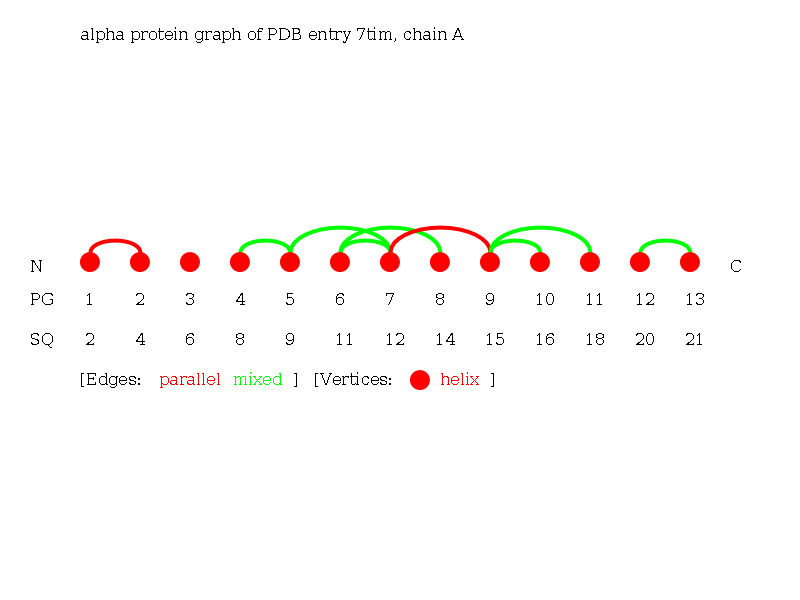
Beta Graph
The Beta-Graph of the protein 7tim chain A consisting of 8 strands. Note the beta barrel in the protein, which is clearly visible as a circle of parallel beta-strands in this graph.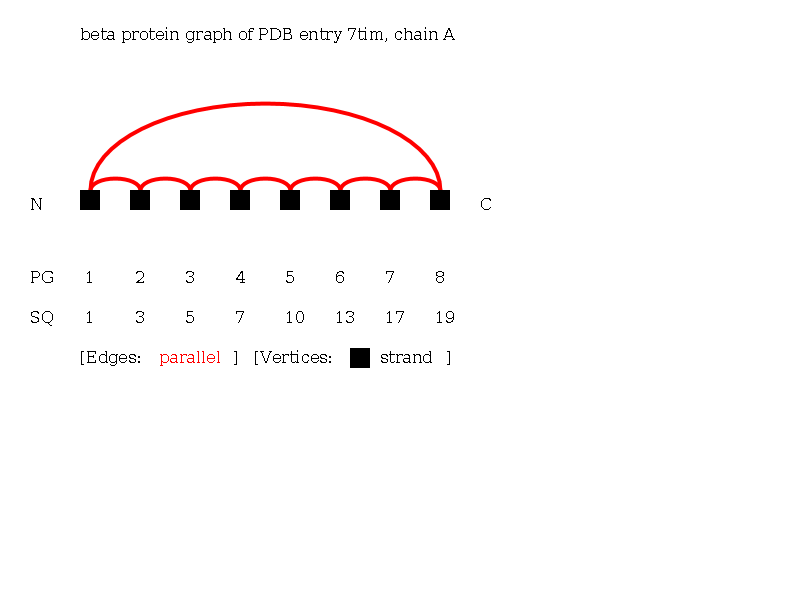
Alpha-Beta Graph
The Alpha-Beta Graph of the protein 7tim chain A consisting of 21 secondary structure elements (13 helices and 8 strands).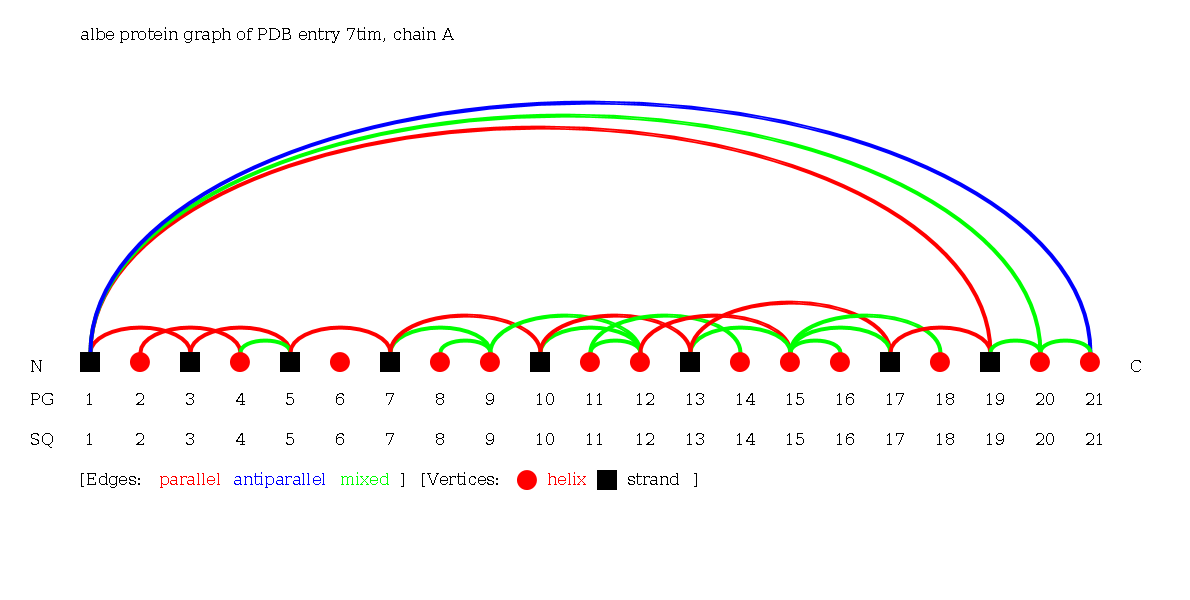
Alpha-Ligand Graph
The Alpha-Ligand Graph of the protein 7tim chain A consisting of 13 helices and 1 ligand.
Beta-Ligand Graph
The Beta-Ligand-Graph of the protein 7tim chain A consisting of 8 strands and 1 ligand.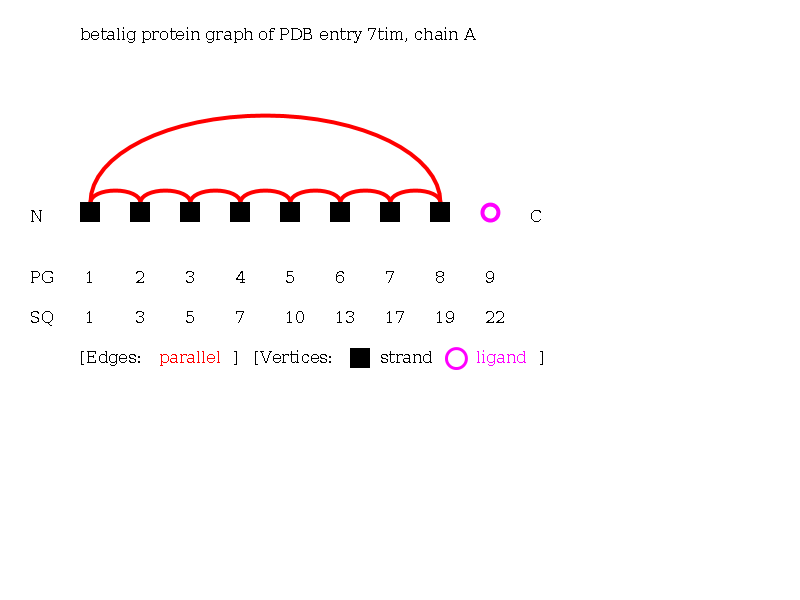
Alpha-Beta-Ligand Graph
The Alpha-Beta-Ligand Graph of the protein 7tim chain A consisting of 22 secondary structure elements (13 helices, 8 strands and 1 ligand).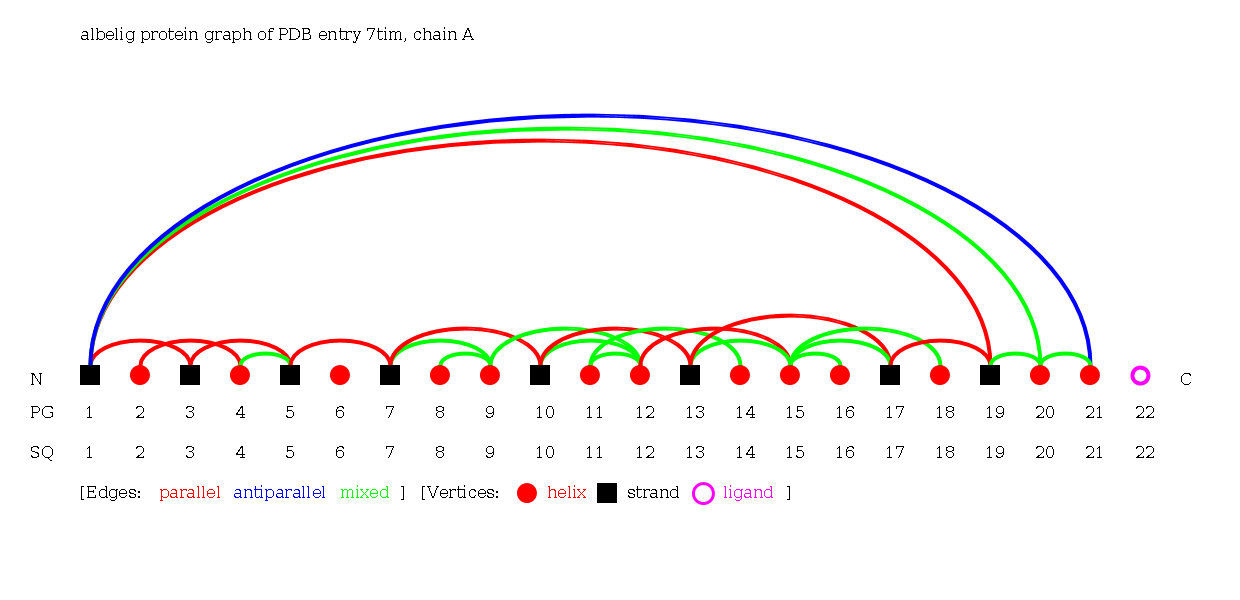
Folding Graphs
A connected component of a Protein Graph is called Folding Graph. Folding Graphs are denoted with capital letters in alphabetical order according to their occurrence in the sequence, beginning at the N-terminus. Folding Graphs consisting of only one secondary structure element are found mostly at the protein surface and not in the protein core. Especially in beta-sheet containing Folding Graphs, the maximal vertex degree of the Folding Graphs is rarely larger than two. Thus, we distinguish between so-called bifurcated and non-bifurcated topological structures. A Protein Graph or a Folding Graph is called bifurcated, if the vertex degree is greater than two, and called non- bifurcated otherwise.
Visualization
In the graph visualizations available on the PTGL server, Folding Graphs follow the Protein Graph visualization. The footer additionally contains the number of the secondary structure element in the Folding Graph (FG).
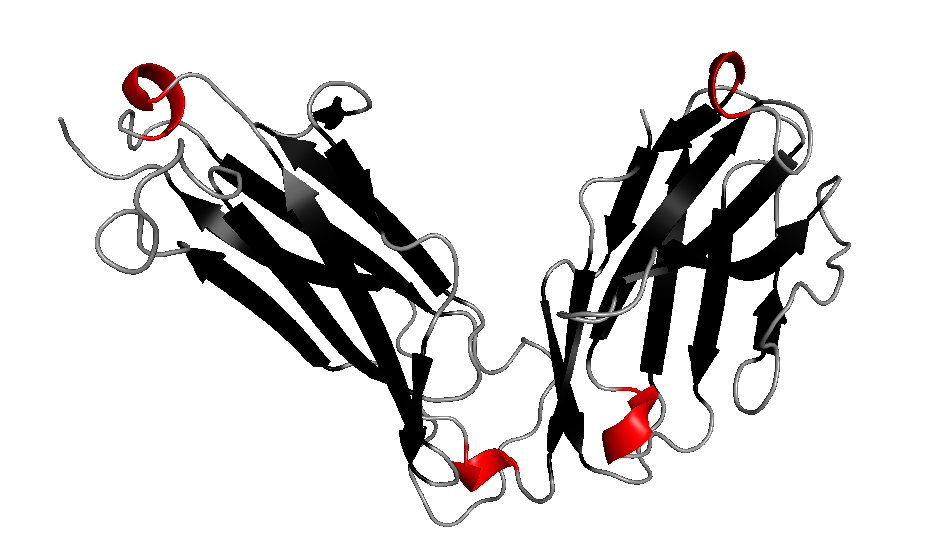
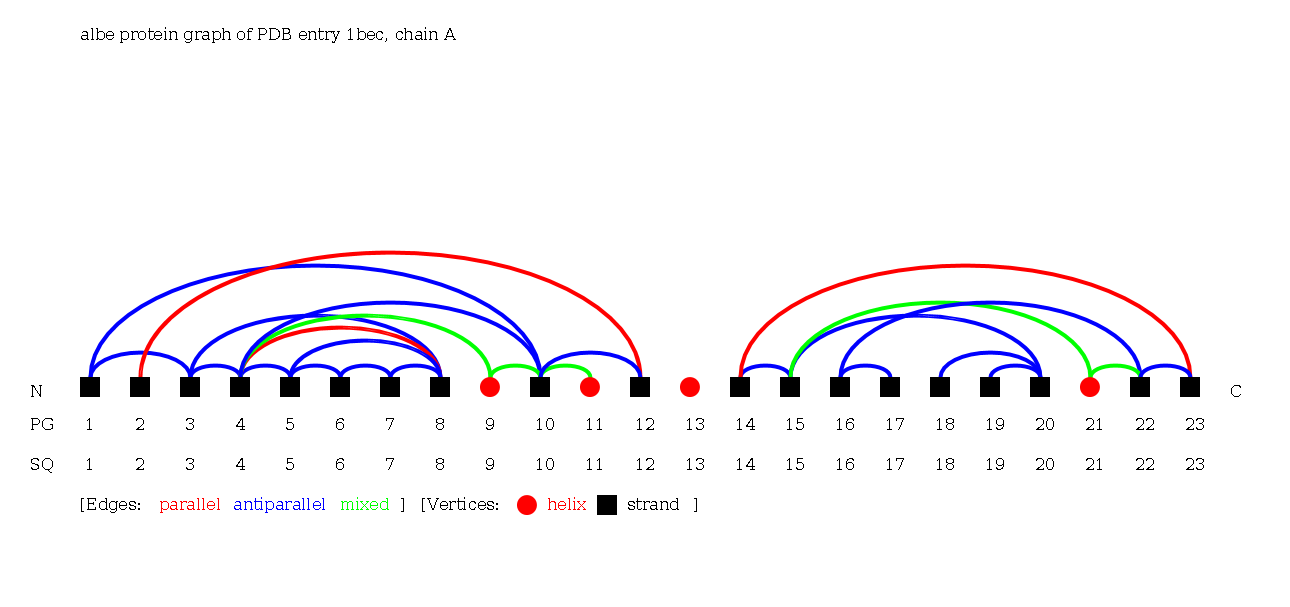
As an example we present an antigen receptor protein structure with PDB ID 1bec [Bentley et al., 1995, Science]. 1bec is a transport membrane protein that detects foreign molecules at the cell surface. The protein consists of one chain A and exhibits three Folding Graphs. It has two domains, which are represented by the Folding Graphs A and C, which are mainly built by strands. Two Folding Graphs (Folding Graphs 1bec_A and 1bec_C) are large enough to be of interest, and one Folding Graph (1bec_B) consists only of a single helix (see Protein Graph of 1bec: helix 13).
3D structure of 1bec:
Alpha-Beta Protein Graph of 1bec:
Alpha-Beta Folding Graph A of 1bec:

Alpha-Beta Folding Graph C of 1bec:
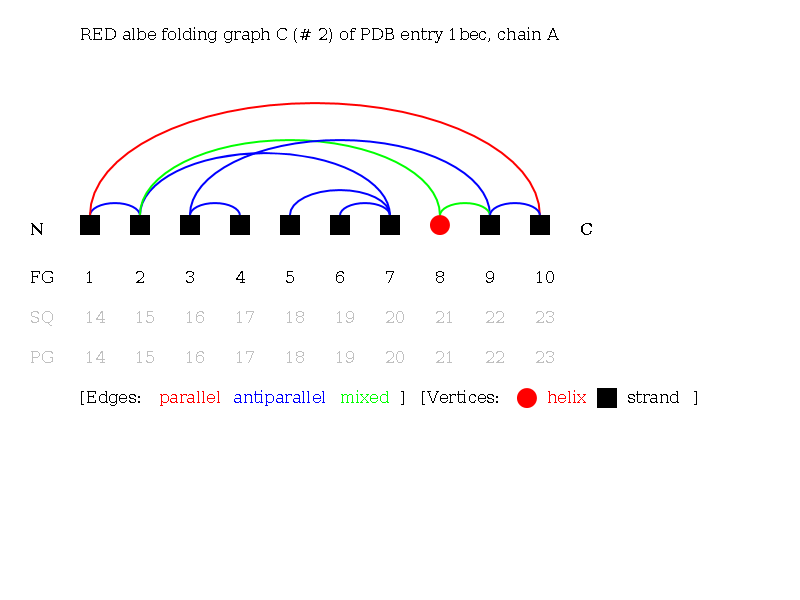
Linear Notations
A notation serves as a unique, canonical, and linear description and classification of structures. The notations for Folding Graphs resemble a protein structure as a linear sequence of secondary structure elements and describe the arrangement of secondary structure elements uniquely. Linear notations enable you to search the PTGLweb for protein motifs. Searching for a structure, SQL-based string matching in the linear notation strings is used to find all Folding Graphs which match the query.
The linear notations are written in different brackets:
- [] denote non-bifurcated Folding Graphs,
- {} denote bifurcated Folding Graphs, and
- () denote barrel structures.
Secondary structure elements are denoted by single characters:
- h denotes helices,
- e denotes strands, and
- l denotes ligands.
- z denotes a special "jump" to a vertex without representing an edge. In case of bifurcated Folding Graphs this may be required to traverse, i.e. enumerate, all vertices, even if there are multiple vertices with an uneven vertex degree.
Edges are completely described by the start and end vertex and their label, i.e., parallel, antiparallel, mixed or ligand. The start and end vertex are saved implicitly as the linear notation traverses the graph and only saves in which direction, i.e. "+" towards C-terminus and "-" towards N-terminus, the edge goes. Edge labels are denoted by single characters:
- p denotes parallel,
- a denotes antiparallel,
- m denotes mixed, and
- j denotes ligand edges.
Notation types
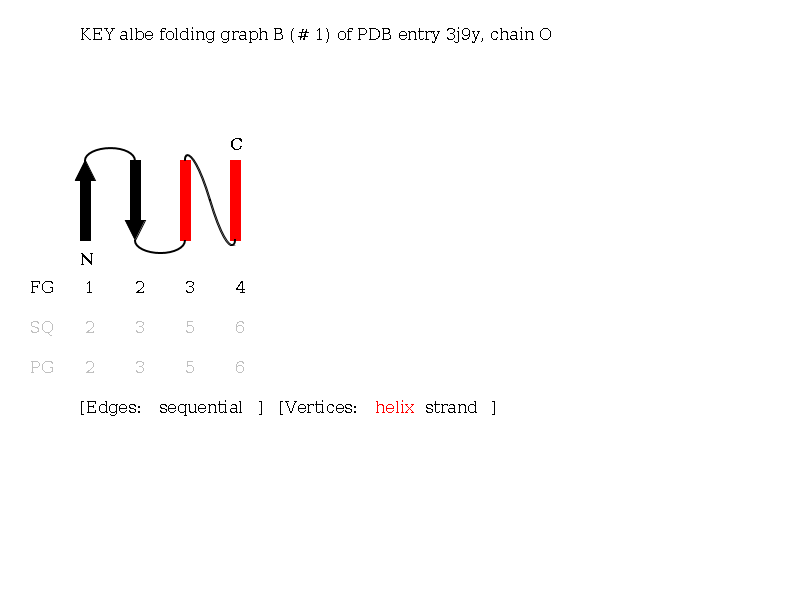
There are two possibilities of representing Folding Graphs: first, one can order the secondary structure elements in one line according to their occurrence in sequence, or second, according to their occurrence in space. In the first case, the adjacent (ADJ), the reduced (RED), and the sequence (SEQ) Folding Graphs, secondary structure elements are ordered as points on a straight line according to their sequential order from the N- to the C-terminus. In the second case, the key (KEY) Folding Graph, secondary structure elements are represented as red rectangles and black arrows for helices and strands, respectively. They are ordered in a straight line corresponding to their spatial arrangement. This is difficult, because in most proteins, secondary structure elements exhibit more than two spatial neighbours. Therefore, KEY Folding Graphs can only be drawn for non-bifurcated Folding Graphs.
Folding Graphs for the different graph types can be derived from the different Protein Graph types: alpha, beta, alpha-beta, alpha-ligand, beta-ligand and alpha-beta-ligand.
Adjacent (ADJ) Folding Graphs
Secondary structure elements are ordered by their occurence in the sequence, from N- to C-terminus. All vertices of the Protein Graph are considered in the adjacent notation of a Folding Graph. This means that adjacent Folding Graphs account for secondary structure elements laying between the secondary structure elements of the Folding Graph without being connected to one of them. Vertices of the Protein Graph that are unconnected to vertices of the Folding Graph are colored grey.
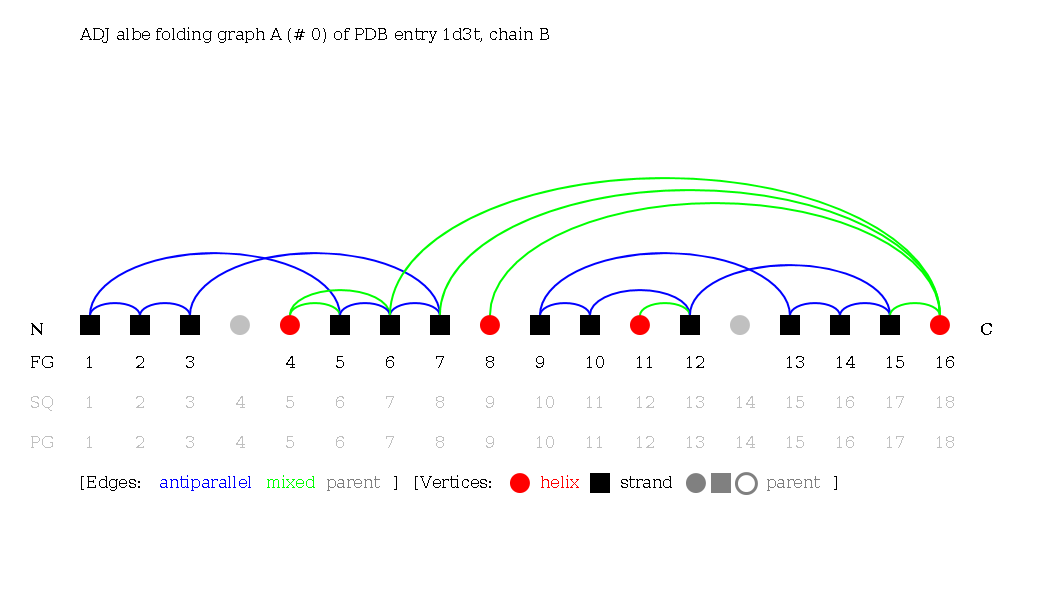
Reduced (RED) Folding Graphs
Secondary structure elements are ordered by their occurence in the sequence, from N- to C-terminus. Reduced Folding Graphs are the same as adjacent Folding Graphs, but only those secondary structure elements part of the Folding Graph are considered.
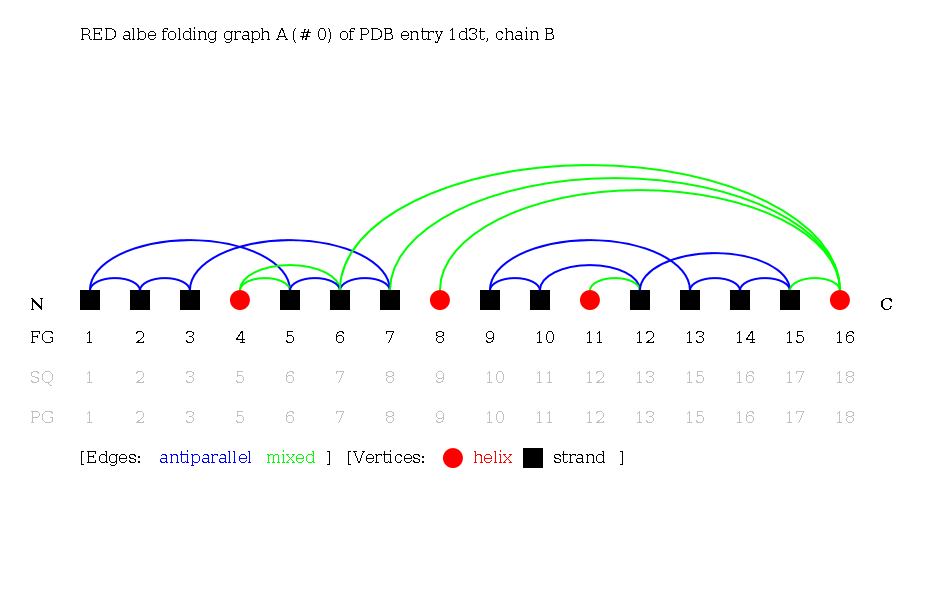
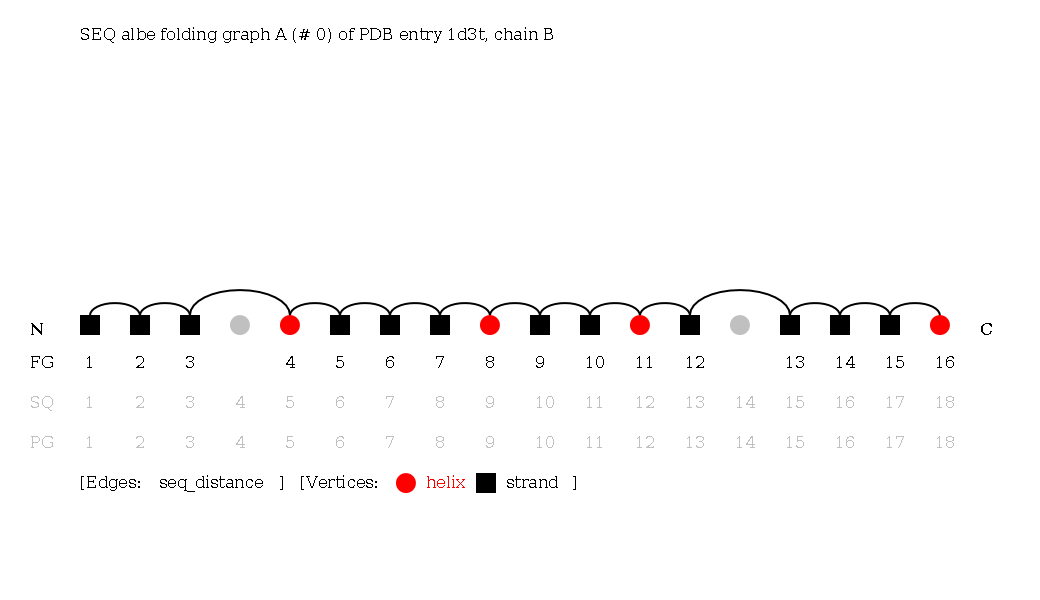
Sequential (SEQ) Folding Graphs
Secondary structure elements are ordered by their occurence in the sequence, from N- to C-terminus. Sequential Folding Graphs are the same as adjacent Folding Graphs, but the edges stand for sequential instead of spatial neighborhood. Because vertices from the Protein Graph that are unconnected to vertices of the Folding Graph are included, but left out from the sequential neighborhood consideration, they are bypassed in the sequence of edges.
Although the sequence notation is trivial, the graphs can be useful, for example, searching for ψ-loops requires a special SEQ notation.
KEY Folding Graphs
KEY Folding Graphs can only be created for non-bifurcated Folding Graphs. KEY Folding Graphs are very close to the topology diagrams of biologists, e.g. Brändén and Tooze (1999). Topologies are described by diagrams of black arrows for strands and red rectangles for helices. As in reduced Folding Graphs, only secondary structure elements of the Folding Graph are considered. Secondary structure elements are ordered spatially and connected in sequential order. See the KEY Folding Graph of the Alpha-Beta Folding Graph B of a histocompatibility antigen 1iebB. The Folding Graph consists of three helices and four strands. This topology exhibits one cross-over connection from helix 6 to helix 7 and forms an Alpha-Beta barrel structure.
Linear notation characteristics: If the arrangement of secondaray structure elements is parallel, an x is noted (Richardson, 1977). In this case, the protein chain moves to the other side of the sheet by crossing the sheet (cross over). Antiparallel arrangements are called same end and are more stable (Chothia and Finkelstein , 1990). Mixed arrangements are defined as same end.
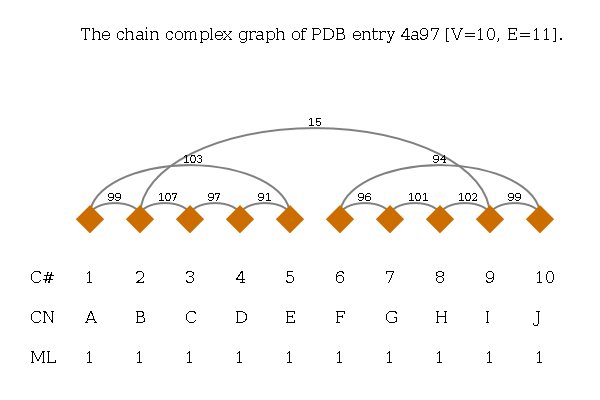
Complex Graphs
A Complex Graph is defined as undirected graph. The vertices correspond to protein chains and are named by their author-provided chain ID from the PDB file. Edges denote a spatial contact and the edge weight corresponds to the number of residue-residue contacts. Below the graph there is a label per vertex for the number of the vertex (C#), chain name (CN) and its molecule identifier (ML).
Motifs
A motif is a common supersecondary structure. A motif consists of only a few secondary structure elements, and it may occur with very different functions. PTGLweb implements motif detection in Protein Graphs for some chosen motifs based on the linear notations of folding graphs. This enables the search for all chains containing one of the predefined motifs. If you want to search for an arbitrary arrangement of secondary structure elements, use the linear notation search.
Alpha motifs
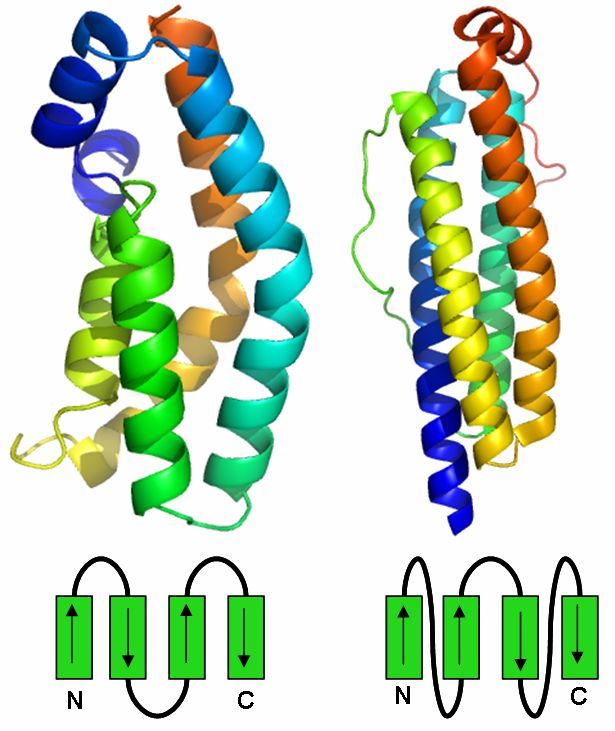
Four Helix Bundle
The Four Helix Bundle is a protein motif which consists of four alpha helices which arrange in a bundle.
There are two types of the Four Helix Bundle which differ in the connections between the alpha helices.
The first type of the Four Helix Bundle is all antiparallel and the second type has two pairs of parallel helices which have an antiparallel connection.
Found 0 times in the current database.
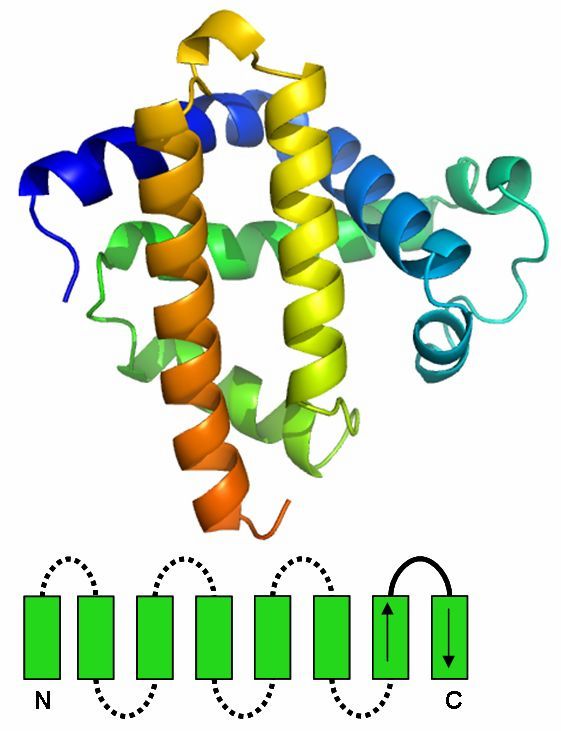
Globin Fold
The Globin Fold is an alpha helix structure motif which is composed of a bundle, consisting of eight alpha helices, which are connected over short loop regions.
The helices do not have a fixed arrangement, but the last two helices in sequential order are antiparallel.
Found 0 times in the current database.
Beta motifs
Up-and-down barrel
The up-and-down barrel is composed of a series of antiparallel beta strands which are connected via hydrogen bonds.
There are two major families of the up-and-down barrel, the ten-stranded and the eight-stranded version.
Found 0 times in the current database.
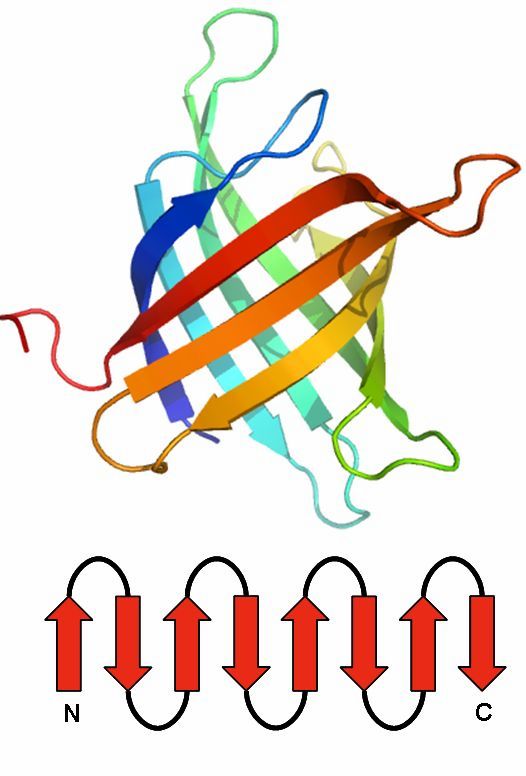
Immunoglobin fold
The immunoglobulin fold is a two-layer sandwich.
Usually, it consists of seven antiparallel beta strands, arranged in two beta sheets.
The first is composed of four and the second of three strands.
Both are connected via a disulfide bond to build the sandwich.
Found 0 times in the current database.
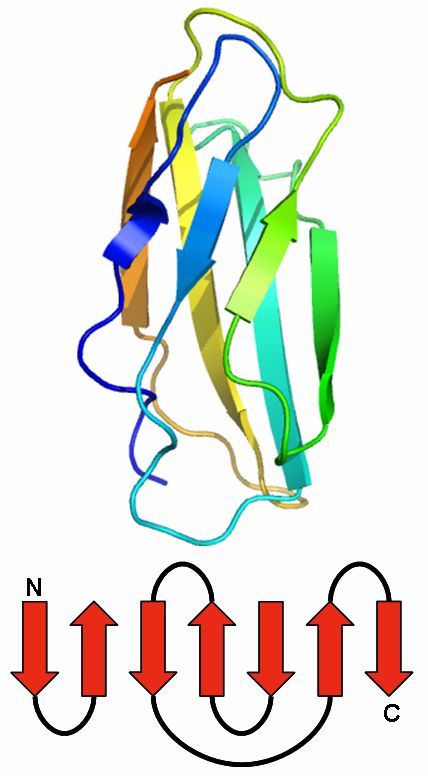
Beta Propeller
This beta motif contains between four and eight beta sheets, which are arranged around the center of the protein.
Each sheet is formed by four antiparallel beta strands.
One sheet makes up one of the propeller blades.
To build a four-bladed propeller, for example, four of these sheets are grouped together.
Found 0 times in the current database.
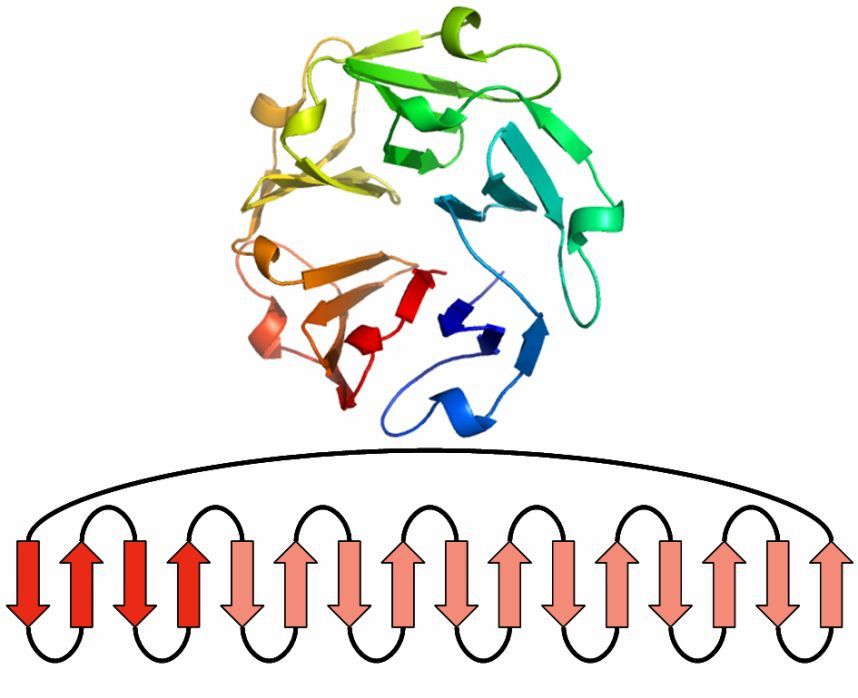
Jelly Roll
The Jelly Roll motif has a barrel structure, which seems like a jelly roll.
The barrel includes eight beta strands, which build a two-layer sandwich of four strands.
Found 0 times in the current database.

Publications
- Wolf JN, Keßler M, Ackermann J, Koch I (2020). PTGL: extension to graph-based topologies of cryo-EM data for large protein structures. Bioinformatics. (DOI 10.1093/bta706 at Oxford University Press).
- Koch I and Schäfer T (2018). Protein super-secondary structure and quaternary structure topology: theoretical description and application. Current opinions in structural biology, 50, 134-143
- Schäfer T, Scheck A, Bruneß D, May P, Koch I (2015). The new protein topology graph library web server. Bioinformatics. (btv574 at oxfordjournals.org).
- Koch I, Kreuchwig A, May P (2013). Hierarchical representation of supersecondary structures using a graph-theoretical approach. Journal of Methods in molecular biology 2013;932:7-33. (/pubmed/22987344).
- Schäfer T, May P, Koch I (2012). Computation and Visualization of Protein Topology Graphs Including Ligand Information. German Conference on Bioinformatics 2012; 108-118. (DROPS).
- May P, Kreuschwig A, Steinke T, Koch I (2009). PTGL - a database for secondary structure-based protein topologies. Nucleic Acids Research, 10.1093/nar/gkp980 (Database issue 2010).
- May P, Barthel S, Koch I (2004). PTGL - Protein Topology Graph Library. Bioinformatics 20(17):3277-3279.
- Koch I, Lengauer T (1997) Detection of distant structural similarities in a set of proteins using a fast graph-based method. Proceedings of the Fifth International Conference on Intelligent Systems for Molecular Biology, 21.-26 Juni, Halkidiki, Greece AAAI Press, California. eds. T. Gaasterland, P. Karp, K. Karplus, C. Ouzounis, C. Sander, A. Valencia:167-187.
- Koch I, Wanke E, Lengauer T (1996) An algorithm for finding maximal common subtopologies in a set of proteins. Journal of Computational Biology 3(2):289-306.
- Koch I, Kaden F, Selbig J (1992) Analysis of Protein Sheet Topologies by Graph Theoretical Methods. Proteins: Structure, Function, and Genetics 12:314--323.
- Kaden K, Koch I, Selbig J (1990) Knowledge-based prediction of protein structures. Journal of Theoretical Biology 147(1):85-100.
Next section
Step-by-step guide